Attention Mechanism

Attention Mechanism

Ref: 딥 러닝을 위한 자연어 처리 입문

Note

my own summary

현재 디코더의 시점 t에서 단어를 예측하기 위해 인코더의 모든 은닉 상태 각각이 디코더의 현 시점의 은닉 상태와 얼마나 유사한지를 판단하는 스코어 값인 어텐션 스코어를 이용하여 인코더의 문맥context를 포함한 값을 입력으로 넣어 정확도를 높이는 방법

RNN에 기반한 seq2seq 모델의 문제점

1. 하나의 고정된 크기의 벡터에 모든 정보를 압축하려고 하니까 정보 손실이 발생
2. RNN의 고질적인 문제인 기울기 소실 문제 존재

\(\to\) 기계 번역 동안 입력 문장이 길면 품질이 떨어지는 현상 발생, 이의 대안으로 입력 시퀀스가 길어지면 출력 시퀀스의 정확도가 떨어지는 것을 보정해주기 위해 들장한 어텐션.

Note

• 그레디언트 기반의 학습에서 역전파할때 발생하는 문제로 0 근처의 숫자를 계속 곱하여 터지거나 0으로 가는 상황

• 그레디언트 기반의 학습

  • 소실함수의 기울기를 통하여 업데이트하는 방식

• 역전파

  • 손실함수를 여러 단계로 쪼갠다(여러 합성 함수로 표현한다).
  • 각 단계의 미분값을 구한다,
  • 그것들을 모두 곱하여 기울기를 계산한다.

참고: 빅데이터 분석 12주차

Attention Function

flowchart LR
    subgraph "Source"
        subgraph B2
            direction BT
            Key1 --> Value1
            Key2 --> Value2
            Key3 --> Value3
        end
    end
  Query --> Source --> Attention\nValue

\[Attention(Q, K, V) = \text{Attention Value}\]

1. 주어진 쿼리에 대해서 모든 키와의 유사도를 각각 구한다.
2. 구한 유사도를 키와 맵핑되어 있는 각각의 값value에 반영한다.
3. 유사도가 반영된 값을 모두 더해서 리턴한다. 여기서 값 = 어텐션 값 attention value

어텐션 모델의 요소

• Q= Query
  • t 시점의 디코더 셀에서의 은닉 상태
• K = Keys
  • 모든 시점의 인코더 셀의 은닉 상태들
• V = Values
  • 모든 시점의 인코더 셀의 은닉 상태들

Dot-Product Attention

• 디코더의 마지막 LSTM 셀이 출력단어를 예측하기 위해 인코더의 모든 입력 단어들의 정보를 다시 참고하고자 함
• 이 때, 소프트 맥스를 이용
  • 인코더에 입력된 값들이 출력 단어를 예측할 때 얼마나 도움이 되었는지 수치화한 결과
  • 다시 디코더로 전달
  • 디코더가 출력 단어를 더 정확하게 예측하게 도와줌

1. 어텐션 스코어를 구한다.

• 인코더의 은닉 시점 time stamp = \(1,2, \dots, N\)
• 인코더의 은닉 상태 hidden state = \(s_t\)
  • 단, 인코더와 디코더의 은닉 상태는 차원이 같음

Important

디코더의 현재시점 t에서 필요한 입력값

seq2seq

• 이전 시점인 t-1의 은닉 상태
• 이전 시점 t-1에서 나온 출력 단어

attention

• 이전 시점인 t-1의 은닉 상태
• 이전 시점 t-1에서 나온 출력 단어
• 어텐션 값 \(a_t\)

attention score 어텐션 값

• 현재 디코더의 시점 t에서 단어를 예측하기 위해 인코더의 모든 은닉 상태 각각이 디코더의 현 시점의 은닉 상태 \(s_t\)와 얼마나 유사한지를 판단하는 스코어 값

닷 프로덕트 어텐션은 은닉 상태 \(s_t\)를 전치(transpose)하고, 각 은닉 상태와 내적(dot product)를 수행하여 스칼라 결과 어텐션 스코어 score 추출

• 닷 프러덕트 어텐션이라고 부르는 이유

\[score(s_t, h_i) = s_t^\top h_i\]

\[e^t = [s_t^\top h_1, \dots, s_t^\top h_N]\]

\(e^t\)는 \(s_t\)와 인코더의 모든 은닉 상태의 어텐션 스코어의 모음값

2. 소프트맥스 함수를 통해 어텐션 분포를 구한다.

• \(e^t\)에 소프트맥스 함수 적용해서 합이 1이 되는 확률 분포 도출
  • 각각 값은 어텐션 가중치 Attention weight
  • 분포는 어텐션 분포 Attention Distribution \(\alpha^t\)

\[\alpha^t = softmax(e^t)\]

3. 각 인코더의 어텐션 가중치와 은닉 상태를 가중합하여 어텐션 값을 구한다.

• 어텐션의 최종 결과값을 얻기 위해 각 인코더의 은닉상태 \(s_t\)와 어텐션 가중치 값attention weight를 곱하고 가중합weighted sum인 어텐션 값attention value \(a_t\)을 구한다.

\[a_t = \sum^N_{i=1} \alpha_i^t h_i\]

Tip

어텐션 값 attention value \(a_t\)는 인코더의 문맥을 포함하고 있다고 하여 컨텐스트 벡터 context vector라고도 부른다.

단, seq2seq에서는 인코더의 마지막 은닉 상태를 컨텍스트 벡터context vector라고 불렀음.

4. 어텐션 값과 디코더의 t 시점의 은닉 상태를 연결한다.

• 어텐션 값\(a_t\)와 디코더의 은닉 상태 \(s_t\)를 결합concatenate하여 하나의 벡터로 만드는 작업을 수행한다. \(\to\) \(v_t\)
• 아 \(v_t\)를 예측 연산의 입력으로 사용함으로써 인코더로부터 얻은 정보를 활용하여 \(\hat{y}\)를 더 잘 예측할 수 있게 됨 \(\to\) 어텐션 메커니즘의 핵심

5. 출력층 연산의 입력이 되는 \(\tilde{s}_t\)를 계산한다.

• 어텐션 값과 디코더의 t시점의 은닉 상태를 연결하고\(a_t s_t\) tanh하이퍼볼릭탄젠트 함수를 통과하도록 해서 출력층 연산을 위한 새로운 벡터 \(\tilde{s}_t\)를 얻는다.

Note

seq2seq

• 출력층의 입력이 t시점의 은닉 상태인 \(s_t\)

attention

• 출력층의 입력이 \(\tilde{s}_t\)

\[\tilde{s}_t = tanh(W_c[a_t;s_t] + b_c\]

\(b_c\)는 편향

참고: 기계학습 특강 9주차 tanh

import torch
import pandas as pd
import matplotlib.pyplot as plt

tanh = torch.nn.Tanh()

_x = torch.linspace(-5,5,100)
plt.plot(_x,tanh(_x))
plt.title("tanh(x)", size=15)

Text(0.5, 1.0, 'tanh(x)')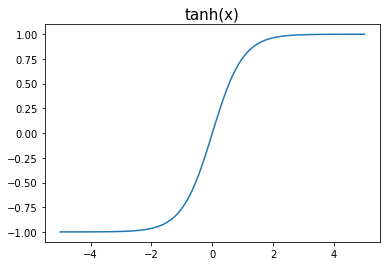

6. \(\tilde{s}_t\)를 출력층의 입력으로 사용한다.

\[\hat{y}_t = Softmax(W_y \tilde{s}_t + b_y)\]

다양한 종류의 어텐션

\(s_t\)는 query, \(h_i\)는 keys, \(W_a\), \(W_b\)는 학습 가능한 가중치 행렬

이름	스코어 함수	defined by
dot	\(score(s_t,h_i) = s_t^\top h_i\)	Luong et al. (2015)
scaled dot	\(score(s_t,h_i) = \frac{s_t^\top h_i}{\sqrt{n}}\)	Vaswani et al. (2017)
general	\(score(s_t,h_i) = s_t^\top W_a h_i\) 단, \(W_a\)는 학습 가능한 가중치 행렬	Luong et al. (2015)
concat	\(score(s_t, h_i) = W_a^\top tanh(W_b[s_t;h_i]),score(s_t,h_i) = W_a^\top tanh(W_b s_t + W_c h_i)\)	Bahdanau et al. (2015)
location-base	\(\alpha_t = softmax(W_a s_t)\) \(\alpha_t\) 산출 시에 \(s_t\)만 사용하는 방법	Luong et al. (2015)